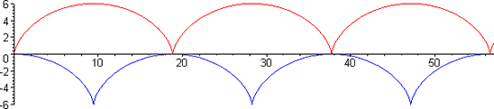
Es una curva plana engendrada por un punto fijo sobre una circunferencia cuando ésta, rueda sin deslizar sobre una recta.

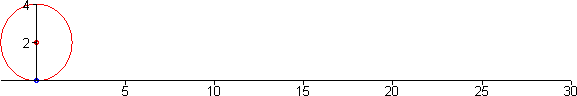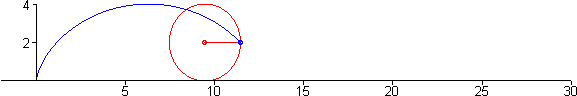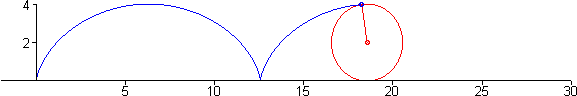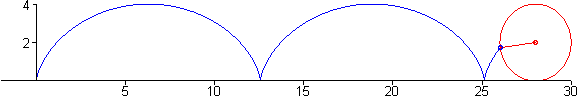
Sus ecuaciones paramétricas son:

Sea P(x,y) un punto genérico de la cicloide y r el radio del círculo generador.

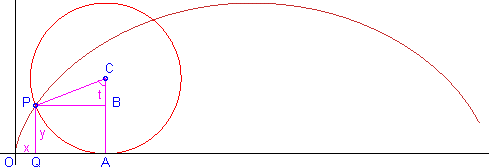
Tomamos como parámetro el á ngulo t que forma el radio CP con la vertical AC

El arco AP es rt e igual al segmento OA, y de la figura podemos deducir:

x=OQ=OA-QA=rt-r sen t=r(t-sent)

y=AB=AC-BC=r-r cos t=r(1-cost).

Por tanto las ecuaciones paramé tricas de la cicloide son:

Esta curva desempeñó un papel importante en el desarrollo histórico de la mecánica. Fue Galileo quien la denominó cicloide y propuso su arco para su uso en arquitectura como modelo para los arcos de un puente, la cicloide es el arco de mayor resistencia estructural. Roberval y Fermat también se ocuparon de ella y Pascal le dedicó en 1658 un notable ensayo. Ese mismo año Wren rectificó la curva.
Huygens descubrió una curiosa propiedad acerca de esta curva:
Sobre un arco de cicloide invertida, un objeto (una canica,..) abandonado a su propio peso, en ausencia de rozamiento, se deslizará desde cualquier punto al punto más bajo exactamente en el mismo tiempo independientemente del punto de partida.

Fue también Huygens, en 1673, quien descubrió su evoluta: otra cicloide igual a la dada obtenida por traslación a partir de ella.
En esta figura vemos la cicloide (línea roja) y su evoluta (línea azul).

La cicloide suscitó gran interés y diversas polémicas entre los científicos del siglo XVII. Su belleza y sus propiedades hicieron que esta curva fuese llamada la Helena de la geometría.