Dadas dos curvas tangentes, si fijamos una de ellas y hacemos rodar la otra sobre la fija, los diversos puntos de la móvil o invariablemente unidos a ella, describen curvas llamadas ruletas. |
|
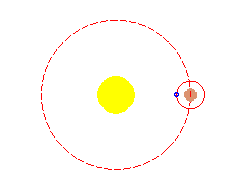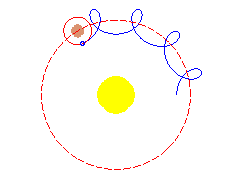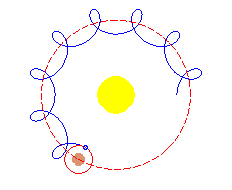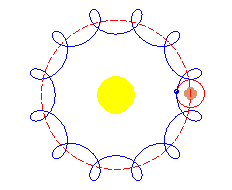 |
Hiparco (190-120 a. C.), trató de explicar los complicados movimientos de los planetas (tomando como referencia la Tierra) suponiendo que describían epicicloides (ruletas en las que la curva fija y la móvil son circunferencias). |
Galileo propuso usar cicloides (ruletas en las que la línea fija es una recta y la que rueda sobre ella una circunferencia) en arquitectura ya que la cicloide es el arco de mayor resistencia estructural. Huygens descubrió una curiosa propiedad acerca de esta curva:
"Sobre un arco de cicloide invertida, un objeto abandonado a su propio peso, en ausencia de rozamiento, se deslizará desde cualquier punto al punto más bajo exactamente en el mismo tiempo independientemente del punto de partida". |
|
