fractales2b

Actividades Didácticas I

1.-

(*) Describir la construcción del fractal árbol de forma que cualquier compañero pueda repetir el dibujo siguiendo tus instrucciones.

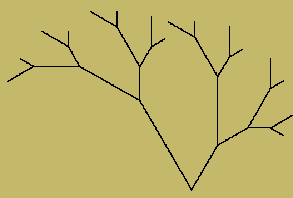
Fractal Árbol

Y dibuja los dos primeros niveles. ¿A qué nivel corresponde la figura anterior?

2.-

(*) Describir la construcción de este nuevo árbol

Dibuja el nuevo árbol de nivel 4

Si el nuevo árbol de nivel 1 está formado por una rama de longitud 2 y dos de longitud 1. ¿Por cuántas ramas y de qué longitud estará formado el nuevo árbol de nivel 4?

3.-

(*) Observa la curva de Koch o cristal de nieve y completa el siguiente cuadro:

Nivel	1	2	3	4
Número de Vértices	3	3+3.3=12
Número de lados	3	3.4=12
Longitud de un lado	1	1/3
Perímetro de la figura	3	4
Área de la figura		A + A/3

(**) A partir de los datos obtenidos en la tabla anterior encuentra una fórmula general para calcular el área y el perímetro de la curva de Koch de nivel n. ¿Cuál es la longitud y área limitada por la curva de Koch?

4.-

(**) Calcula el área limitada por la curva anticristal de nieve.

5.-

(***) Como ya sabes si una función es derivable en un punto x₀ entonces es continua en dicho punto. El recíproco de este teorema no siempre es cierto como podemos ver con la función y=lxl, que es continua en el origen pero no es derivable en dicho punto. Tanto el cristal como el anticristal de nieve representan casos "patológicos" de funciones que son continuas en todos sus puntos y no son derivables en ninguno de ellos. ¿Sabrías indicar otras funciones que cumplan la misma propiedad?

6.-

(**) Describe el proceso seguido para construir la curva de Sierpinski. Demuestra que esta curva (que ocupa totalmente el cuadrado en que se inscribe) limita una superficie que es los 5/12 del área del cuadrado.

7.-

(*) Observa el proceso seguido para construir la alfombra de Sierpinski y completa el siguiente cuadro, supuesto que el lado del cuadrado inicial es 1

Nivel	1	2	3	4
Número de cuadrados	2	10
Área de la parte eliminada (en blanco en la figura)
Área de la Alfombra (color rojo)

(**) Deduce una fórmula para calcular el área de la alfombra de Sierpinski de nivel n.