1. (***) Cuando el punto P recorre la circunferencia, ¿sabrías determinar alguna posición especial de la recta de Simson y qué propiedad cumple?
2. (***) Comprueba que la recta de Simson relativa al punto P, equidista de P y del ortocentro.
3. (*) ¿Qué lados corta la recta de Euler en los triángulos acutángulos y obtusángulos?
4. (**) Comprobar que existe un punto P en la recta de Euler del triángulo ABC tal que las distancias de los baricentros de los triángulos ABP, BCP, y ACP a los vértices C, A, y B respectivamente, son iguales entre sí.
5. (**) Comprobar que existe un punto P en la recta de Euler del triángulo ABC tal que las distancias de los baricentros de los triángulos ABP, BCP, y ACP a los vértices C, A, y B respectivamente, son iguales entre sí.
6. (**) Sea K el punto simétrico del centro de la circunferencia circunscrita al triángulo ABC, respecto del lado BC. Demostrar que la recta de Euler del triángulo ABC divide al segmento AK por la mitad.
7. (***) Una buena parte de los símbolos matemáticos que hoy utilizamos fueron introducidos por Euler como i (para la unidad imaginaria i = , para designar la longitud de una circunferencia de diámetro unidad) y e (base de los logaritmos neperianos). A él debemos también la fórmula:

   

   que relaciona los cinco números fundamentales de la matemática.
   Quizás, aún no comprendas demasiado bien qué significan este tipo de expresiones pero puedes consolarte pensando que Benjamín Pierce (1809-1880) -el primer matemático americano de renombre- se hizo una gran fotografía con otra fórmula de Euler en el fondo

   

   De la que solía decir: "Señores, no tenemos la menor idea de lo que esto significa, pero seguro que significa algo muy importante".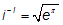
   El número e, como ya has ido viendo en clase, aparece en numerosas situaciones. Por ejemplo, los cables del tendido eléctrico tienen una forma que viene determina por la función: y = e^x + e^-x
   ¿Podrías comprobarlo representando la función anterior?

Con relación a las rectas de Euler y Simson puede consultarse:
DUNHAM, W. (2000) Euler. El maestro de todos los matemáticos. "La matemática en sus personajes, nº 6". Madrid, Nivola.
GUZMAN, M. de, COLERA, J., SALVADOR, A. (1987) Matemáticas 2º B.U.P. Madrid, Ed. Anaya. 
SHARIGUIN, I. (1986) Problemas de Geometría. Planimetría. Moscú, Editorial Mir.