Actividades sobre Curvas Cicloidales
  1. (*) Recorta en cartulina un cuadrado ABCD y hazlo rodar sobre la recta r como indica la figura: primero gira alrededor de A hasta que la arista DC quede horizontal, después alrededor de B, etc. Dibuja con detalle la trayectoria que sigue el punto B. Investiga la trayectoria de otros puntos. Prueba con otros polígonos. (triángulos,...).(sitúa el ratón sobre la figura que hay bajo estas líneas)
    pasa el ratón
  2. (*) Señala un punto en una circunferencia, hazla rodar sobre una recta y dibuja la trayectoria que describe ese punto. Utiliza para ello los materiales que creas conveniente, podría ser una moneda y una regla o una lata cilíndrica, sin tapa, con una mina pegada en su interior. Al hacerla rodar sobre una mesa la mina dibujará la curva sobre una hoja de papel colocada en la pared o en un libro en posición vertical.
  3. (*) Construye una pista cicloidal y otra rectilínea (suficientemente largas) con madera o alambre, u otro material como en la figura. Comprueba experimentalmente que una canica abandonada a su propio peso en el punto A llega antes al punto B por la pista cicloidal que por la rectilínea. Esto sucede por ser la cicloide la curva la de descenso más rápido o "braquistocrona".

  4. (*) Construye cicloides alargadas y acortadas con los materiales que creas oportuno.
  5. (*) Encuentra un método para trazar epicicloides (círculos de cartulina, tapones de corcho,...). Préstale especial atención al caso R=2r, la curva obtenida se llama Nefroide.
  6. (*) Encuentra un método para trazar hipocicloides. ¿Qué condiciones deben cumplirse para que se cierre la curva? Traza una hipocicloide para el caso en que R=3r, la curva obtenida se llama Deltoide. 
  7. (*) Galileo conjeturó que el área encerrada por un arco de cicloide es tres veces la del círculo generador y Roberval corroboró esta conjetura. Compruébalo construyendo dichos recintos con una chapa (de madera, plástico, metal,...) y pésalos. 

    La superficie de cada una de los recintos R1, R2 y R3 es r2. 

  8. (*) Determina la longitud del arco con un hilo enrollado sobre él. Comprueba que equivale a cuatro veces el diámetro del círculo generador.  
  9. (**) Halla las longitudes de los lados de un triángulo equilátero para que, al rodar sobre sus lados un círculo de 2 cm de radio, determine sobre cada uno de ellos un arco completo de cicloide.
  10. (**) La siguiente figura representa una cicloide. Dibuja empleando sólo regla y compás la posición del círculo generador que pasa por el punto P. Explica y justifica con detalle su construcción.
  11. (***) Galileo Galilei sostenía que el movimiento es relativo porque depende del sistema de referencia del observador. En su obra “Dos Nuevas Ciencias” proporcionó un método de resolución para describir movimientos complejos en dos dimensiones, al establecer el principio de independencia de los movimientos. Lo aplicó al movimiento de proyectiles y sentó las bases del cálculo del movimiento de proyectiles. La importancia de su aportación radica en la idea que encierra el principio de independencia de los movimientos, según el cual, cualquier movimiento complejo puede considerarse como una combinación de movimientos, que puede obtenerse sumando los movimientos elementales que lo componen. De otro modo, el principio de independencia de los movimientos de puede enunciarse así:

    Cuando una partícula está dotada de dos movimientos simultáneos, su cambio de posición es independiente de que los dos movimientos actúen de forma sucesiva o de forma simultánea.

    Un caso interesante de movimiento combinado es el movimiento general de un sólido rígido, constituido por una rotación y una traslación que pueden describirse de forma independiente. El movimiento global es la suma de ambos. Algunos de estos movimientos combinados corresponden a las curvas cicloides y ruletas presentadas. Veamos un problema típico: Un velocípedo similar a los que se construían en el siglo XIX se mueve en una superficie horizontal. ¿Cómo es la trayectoria, respecto de un observador inmóvil, de la válvula del neumático delantero?, ¿cómo es la del neumático trasero?; ¿y la del pedal?

    Pulsa sobre la válvula de la figura
    Pulsa sobre el pedal que está sobre la válvula

     

    Una primera aproximación puede obtenerse de forma gráfica mediante una lata cilíndrica. Se fija una mina de lápiz a un punto y se hace rodar sobre una recta (por ejemplo, el canto de una regla fija), de modo que en una cartulina vertical deje la marca de la trayectoria seguida.

    Por otro lado, la resolución analítica del problema es relativamente fácil, si se tiene en cuenta que el movimiento de la válvula o el del pedal es la combinación de dos movimientos: una rotación de velocidad angular constante, en torno al centro de la rueda, y un movimiento de traslación paralelo al suelo. Es el movimiento correspondiente a dos cicloides:
    1. El de la válvula de la rueda delantera (y el de la trasera), es una cicloide natural.
    2. El del pedal es una cicloide acortada, que se asemeja a una curva sinusoidal.
    Las ecuaciones paramétricas de la cicloide natural son:

    x = r(σ – sen σ)
    y = r(σ – cos σ)

    El parámetro σ es la posición angular de la válvula de la rueda, la cual, si lleva un movimiento circular uniforme, viene dada por
    σ = w t, donde t es el tiempo, y w la velocidad angular con que se desplaza la rueda. Se puede poner, dado que rueda sin deslizar, w = v/r, donde v es la velocidad que lleva el centro de la rueda. Las ecuaciones paramétricas se pueden escribir ahora:

    x = v(t – sen t)
    y = v(t – cos t)

    Basta con dar valores a t para obtener los puntos que nos permiten dibujar la cicloide.
  12. En los tiovivos de las ferias y parques de atracciones podemos sentarnos en una olla o taza giratoria, que da vueltas en torno a su centro mientras gira el tiovivo. ¿Cómo es la trayectoria del pasajero para un observador situado en el suelo, fuera del tiovivo?
    El problema se resuelve sin complicaciones si se tiene en cuenta que se trata de una epicicloide, en el que hay una superposición o combinación de giros:
    • Uno exterior en torno a un punto fijo a la plataforma del tiovivo.
    • Otro en torno al centro de la plataforma del tiovivo (al que va unida la olla giratoria), que suele llamarse "movimiento deferente".
    La diferencia entre un movimiento epicíclico normal estriba en que la velocidad de giro deferente no está relacionada con la velocidad del giro epicíclico.
    Los filósofos griegos habían dado una descripción heliocéntrica del movimiento planetario poco precisa, entre otras razones, porque describían los movimientos de los cuerpos celestes como movimientos circulares simples (lo que se conoce como teoría de las esferas homocéntricas de Eudoxo (408-355 a. C.) y Calipo (330 a. C.). El modelo fue perfeccionado por Hiparco (190-120 a. C.), el cual trató de explicar los complicados movimientos de los planetas (tomando como referencia la Tierra) suponiendo que describían epicicloides. El modelo fue completado por Claudio Ptolomeo (85-165 d.C.) en su tratado de astronomía Almagesto, que perduró 14 siglos.

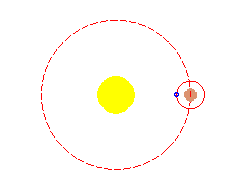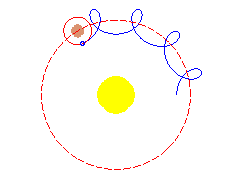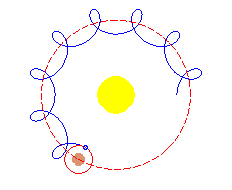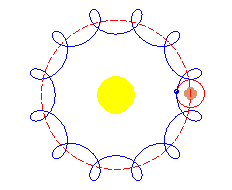
    El epicicloide descrito por un cuerpo celeste, según Hiparco, es la combinación de dos movimientos: un movimiento circular del planeta en torno a un punto (epiciclo), que a su vez, gira en una órbita circular, también con movimiento uniforme (movimiento deferente), pero en sentido opuesto.

CicloidesReferencias
pulsar pulsar